cristallographie (suite)

Exemple de structure atomique

On peut connaître la position de tous les atomes dans le milieu cristallin si l’on connaît, d’une part, son réseau, c’est-à-dire les trois périodes 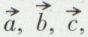qui définissent la maille, et, d’autre part, le motif cristallin, c’est-à-dire le contenu atomique de la maille. Le réseau est fourni sans ambiguïté par les rayons X. Considérons le chlorure de sodium. La maille est cubique, a = b = c = 5,640 Å. Elle contient quatre ions Cl^– et quatre ions Na⁺. Si l’on prend comme origine le centre de gravité d’un ion Cl^–, les quatre atomes Cl ont pour coordonnées numériques : 0 0 0 ; 0 1/2 1/2 ; 1/2 1/2 0 ; 1/2 0 1/2. Le réseau des atomes Na se déduit de celui des Cl par la translation 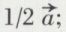les quatre atomes Na ont pour coordonnées numériques : 1/2 0 0 ; 1/2 1/2 1/2 ; 0 1/2 0 ; 0 0 1/2 (fig. 7).

La symétrie cristalline

La notion de symétrie joue un rôle primordial en cristallographie ; elle est à la base de la classification des cristaux ; les formes cristallines, les propriétés physiques, les structures atomiques sont intimement liées à la symétrie. Les opérations de symétrie transforment une figure F en une figure F′ en conservant la longueur d’un segment de droite quelconque dans l’espace à trois dimensions ; elles sont de deux sortes : celles de symétrie directe ou de première espèce, qui amènent la superposition des deux figures F et F′ par un simple déplacement qui est un mouvement hélicoïdal autour d’un axe, c’est-à-dire une rotation suivie d’une translation parallèle à l’axe ; celles de symétrie inverse ou de deuxième espèce, pour lesquelles les figures F et F′, dites énantiomorphes (exemple : mains droite et gauche), ne sont superposables qu’après une inversion par rapport à un point ou une réflexion de l’une d’elles dans un miroir.

Il a fallu tout le xix^e s. pour que les cristallographes formulent la théorie géométrique de la symétrie spatiale. Dans la première partie de ce siècle, les minéralogistes ne se sont intéressés qu’à la symétrie macroscopique pour rendre compte des formes cristallines. Comme, à cette échelle, le cristal est homogène, les éléments de symétrie sont des axes de rotation qui passent par un même point, qui reste fixe au cours des opérations de symétrie. C’est la symétrie ponctuelle ou encore la symétrie d’orientation. La périodicité du milieu cristallin, que traduit la loi d’Haüy, a pour conséquence que les axes de symétrie directe sont des axes A_n d’ordre n, tels que des rotations de 2π/n laissent le cristal inchangé, n est entier et ne peut prendre que les valeurs 1, 2, 3, 4 et 6 ; ces axes sont représentés par les symboles A₁, A₂, A₃, A₄, A₆ ou, plus simplement, par 1, 2, 3, 4, 6. Une face inclinée sur un axe d’ordre n appartient à une forme de n faces équivalentes. On dit que le degré de symétrie directe est n. De même, les opérations de symétrie inverse sont des rotations de 2π/n autour d’un axe passant par le point fixe, combinées chacune à une inversion I par rapport à ce point. C’est l’axe inverse d’ordre n, que l’on désigne par Ā_n, qui implique les deux opérations de rotation et d’inversion, ce que l’on symbolise par Ā_n = A_n . I = I . A_n. Les seuls axes inverses des cristaux sont Ā₁, Ā₂, Ā₃, Ā₄, Ā₆ ou encore Le centre de symétrie a pour symbole Ī ; le plan de symétrie, ou miroir, équivaut à l’axe Ā₂, de sorte qu’il est représenté indifféremment par ou par m.

En combinant ensemble les éléments de symétrie directe et inverse, Johann Friedrich Christian Hessel (1796-1872) a montré, en 1830, que les cristaux se répartissent dans trente-deux classes de symétrie ponctuelle. À chacune d’elles, il correspond un degré de symétrie, qui est le nombre des opérations de symétrie des formes cristallines, ensemble des faces équivalentes et des propriétés physiques caractéristiques. Ce résultat fut retrouvé indépendamment par Bravais en 1849.

Celui-ci rechercha tous les types de symétrie compatibles avec un arrangement régulier et infini des molécules dans les trois dimensions de l’espace. Il établit que les assemblages réguliers de points géométriques remplissant l’espace appartiennent à quatorze modes de réseau, par les nœuds desquels passent les éléments de symétrie de sept parmi les trente-deux classes de symétrie. Ces sept classes de symétrie des réseaux définissent les sept systèmes cristallins : cubique, quadratique, hexagonal, rhomboédrique, orthorhombique, monoclinique, triclinique, et les trente-deux classes de symétrie se répartissent dans ces sept systèmes cristallins. Quand la symétrie du cristal est celle de son réseau, le cristal est dit holoédrique ; quand elle est plus petite, il est mériédrique ; la mériédrie est une hémiédrie, une tétartoédrie ou une ogdoédrie quand le degré de symétrie du cristal est la moitié, le quart ou le huitième de celui de son réseau. Bravais envisageait le milieu cristallin comme un assemblage de « molécules » identiques, de même orientation, disposées aux nœuds d’un des quatorze modes possibles de réseau, et les éléments de symétrie du cristal sont ceux qui sont communs à la fois à la molécule et au réseau. La théorie de Bravais rend bien compte des notions d’holoédrie et de mériédrie. Un observateur qui se déplace d’une molécule à une autre, tout en conservant la même orientation, retrouve la même vision de l’assemblage. Le problème a été ensuite généralisé. Les opérations de symétrie qui amènent les points du milieu cristallin en coïncidence avec des points équivalents (même vision de l’assemblage pour un observateur quelle que soit son orientation) définissent sa symétrie de position ; elles entraînent l’existence d’axes hélicoïdaux et de miroirs translatoires, dont les positions sont bien définies dans la maille. Un axe hélicoïdal A_n,t fait correspondre à un point de la maille n points équivalents de la même maille obtenue par des rotations de 2π/n accompagnées d’une translation 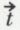parallèle à l’axe. Comme tout axe de symétrie est parallèle à une rangée du réseau, 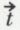ne peut prendre que la valeur étant le vecteur période de la rangée et m un nombre entier qui est l’un des nombres 0, 1, 2,..., n – 1. Ainsi, les axes de symétrie directe d’ordre 4 du milieu cristallin sont les axes 4, 4₁, 4₂ et 4₃. Les miroirs translatoires font correspondre à un point du milieu un point équivalent, dont la position s’obtient par une translation du point image, parallèle au miroir.