cristallographie (suite)

Mais, si un cristal, gêné dans sa croissance, ne présente pas de faces et s’il n’a pas de clivages (c’est le cas du quartz), son anisotropie discontinue se trouve révélée par la diffraction des rayons X ou des électrons ou des neutrons. Un faisceau de rayons X se réfléchit sur des plans du milieu cristallin dont l’orientation est parfaitement définie. Les plans de clivage, les plans réflecteurs des rayons X obéissent, comme les faces naturelles, à la loi de Romé de L’Isle. Toutes ces directions discontinues font partie d’un même faisceau de plans obéissant à des lois arithmétiques précises qui font l’objet de la cristallographie géométrique.

Structure périodique du milieu cristallin, loi d’Haüy

La calcite cristallise sous cent soixante-dix formes différentes, qui peuvent se combiner entre elles pour donner à ce minéral des faciès très différents ; de sorte qu’on a longtemps attribué à la forme des cristaux « un caractère variable, presque accidentel ». C’est l’observation des clivages qui conduisit Haüy, en 1784, à établir sa théorie réticulaire des cristaux. Tous les cristaux de calcite peuvent fournir par clivage un rhomboèdre, parallélépipède dont les six faces sont des losanges égaux, faisant entre elles un angle de 105° 5′. Ce rhomboèdre, qu’Haüy dénomme forme primitive, peut être divisé en rhomboèdres de plus en plus petits. Haüy eut l’idée de supposer une limite à ces divisions successives et d’admettre l’existence d’un solide élémentaire qui ne peut être divisé sans décomposition chimique de la substance. Les cristaux de calcite sont des empilements réguliers de ces solides élémentaires. À partir de la forme du parallélépipède élémentaire et de la loi d’empilement, on peut calculer l’inclinaison des faces cristallines. C’est ce qu’a fait Haüy pour la quasi-totalité des minéraux connus à son époque.

Les figures 3 et 4 montrent la formation du dodécaèdre rhomboïdal et du dodécaèdre pentagonal de la pyrite FeS₂ à partir du cube élémentaire ; si les cubes sont très petits, les escaliers que constituent les différentes couches sont imperceptibles et les faces apparaissent planes. La figure 5 indique la formation du scalénoèdre de calcite, forme fréquente, à partir du rhomboèdre élémentaire.

Ainsi, pour Haüy, tout cristal est un assemblage de petits parallélépipèdes identiques, accolés par leurs faces. Le milieu cristallin possède une triple périodicité suivant les arêtes de ce parallélépipède.

Haüy a exprimé son hypothèse sous une forme traduisant directement les mesures d’angle des faces. Considérons trois faces d’un cristal se coupant suivant trois droites choisies comme axes de référence et une quatrième rencontrant ces axes aux points A, B, C. Les rapports OA/OB et OC/OB sont déterminés par les angles des quatre faces et les grandeurs OA = a, OB = b et OC = c sont les paramètres du cristal, connus seulement par les rapports a : b : c. Une face quelconque coupant les trois axes en A′, B′ et C′ est déterminée en direction si l’on connaît OA/OA′, OB/OB′ et OC/OC′, qui sont les indices (ou paramètres) de la face. La loi des troncatures rationnelles, ou loi d’Haüy, peut s’énoncer ainsi : les faces d’un cristal sont parmi celles dont les indices sont des nombres entiers petits.

Réseaux cristallins

Auguste Bravais (1811-1863) a exprimé la périodicité du milieu cristallin avec les réseaux cristallins. Si 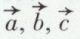sont trois vecteurs définissant le solide (ou maille élémentaire) d’Haüy, le réseau est l’ensemble des points analogues d’un point quelconque du milieu cristallin ; ces points (ou nœuds) du réseau sont obtenus en faisant subir à ce point le groupe de translations x, y et z étant l’ensemble des nombres entiers positifs et négatifs. Chacun des nœuds est défini par trois nombres entiers qui sont ses coordonnées numériques.

Il suffit, pour définir le milieu cristallin, de connaître la nature chimique et la position des atomes contenus dans la maille ; c’est le motif cristallin. On peut se faire une image, tout au moins dans le plan, de la périodicité du milieu en le comparant au motif indéfiniment répété d’un papier de tenture. Ce motif se retrouve en tous les nœuds d’un réseau de parallélogrammes dont les côtés n’ont aucune existence matérielle, tout comme la maille élémentaire d’un cristal. À chaque maille élémentaire, il correspond un seul nœud. On peut être amené, pour des questions de symétrie, à définir le réseau à partir d’une maille multiple d’ordre m, qui comprend m nœuds et dont le volume est m fois le volume d’une maille primitive. Dans ce cas, aux translations (x, y, z étant l’ensemble des entiers), il faut ajouter les translations telles que (x₁, y₁, z₁ étant les nombres fractionnaires définissant la position du nœud x₁ y₁ z₁ à l’intérieur de la maille).

À tout groupe de trois nombres entiers h k l premiers entre eux correspond un faisceau de rangées cristallines que l’on désigne par (h k l) ; il passe une telle rangée par tout nœud du réseau. La période de cette rangée est le vecteur qui joint deux nœuds consécutifs sur la rangée.

On montre qu’à tout groupe de trois nombres entiers premiers entre eux h k l il correspond une famille de plans réticulaires parallèles équidistants, désignés suivant la notation de W. H. Miller par (h k l), dans lesquels entrent tous les nœuds. Ces plans ont pour équations hx + ky + lz = 0 ; ± 1 ; ± 2 ; ... La distance entre deux plans consécutifs est d’autant plus grande que la densité réticulaire, qui est le nombre de nœuds par unité de surface, est plus grande. La stratification multiple des réseaux cristallins ainsi mise en évidence permet d’énoncer la loi d’Haüy-Bravais : les faces naturelles d’un cristal, les plans de clivage sont parallèles à des plans réticulaires et sont d’autant plus importants que la densité réticulaire est plus grande, c’est-à-dire que les indices h k l sont plus petits. La figure 6 indique la disposition des nœuds d’un réseau de prismes droits à base rectangulaire (réseau orthorhombique), défini par les trois vecteurs rectangulaires projetés sur le plan (001). On a mis en évidence l’orientation des plans réticulaires, tous perpendiculaires au plan de la figure et parallèles à l’axe de notations (100), (010), (110), (210), (130). Ces plans réticulaires, parallèles à la rangée [001], sont dits plans en zone ; l’axe de zone est ici la rangée [001].