conique (suite)
7o 2x2 + 3y2 = 0 est l’équation de deux droites imaginaires conjuguées, car elle se décompose sous la forme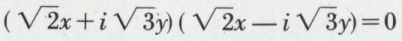
et donne les droites d’équations  et
et 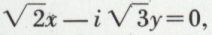 qui sont imaginaires conjuguées, car leurs coefficients sont deux à deux imaginaires conjugués.
qui sont imaginaires conjuguées, car leurs coefficients sont deux à deux imaginaires conjugués.
Réduction des coniques en axes rectangulaires (base orthonormée)
Réduction des coniques à centre
Dans l’équation 
AC – B2 est non nul et la conique correspondante n’est pas du genre parabole. Le centre ω (x0, y0) est fourni par le système fx′ = 0, fy′ = 0 ; on le prend comme nouvelle origine, les formules de changement d’axes étant x = X + x0, y = Y + y0. L’équation (1) devient alors l’équation
avec f = AC – B2. On prend alors comme nouveaux axes les axes ωx′ et ωy′ ayant pour vecteurs unitaires les vecteurs propres de la matrice 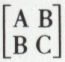 ; cette nouvelle base est orthonormée. L’équation (2) se met sous la forme
; cette nouvelle base est orthonormée. L’équation (2) se met sous la forme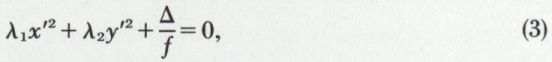
λ1 et λ2 étant les valeurs propres de la matrice 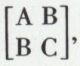 c’est-à-dire les racines de l’équation λ2 – (A + C)S + AC – B2 = 0.
c’est-à-dire les racines de l’équation λ2 – (A + C)S + AC – B2 = 0.
1o Si λ1 et λ2 sont de signes contraires à 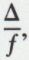 on pose
on pose 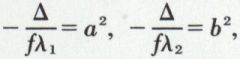 et (3) s’écrit
et (3) s’écrit  qui est l’équation d’une ellipse de demi-axes a et b, respectivement sur ωx′ et ωy′.
qui est l’équation d’une ellipse de demi-axes a et b, respectivement sur ωx′ et ωy′.
2o Si λ1 et λ2 sont du signe de  on pose
on pose  et (3) devient
et (3) devient 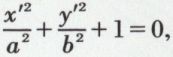 qui est l’équation d’une ellipse imaginaire d’axes ωx′ et ωy′.
qui est l’équation d’une ellipse imaginaire d’axes ωx′ et ωy′.
Dans le cas particulier où λ1 = λ2, on obtient un cercle, réel ou imaginaire.
3o Si λ1 et λ2 sont de signes contraires, en posant soit 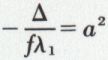 et
et  soit
soit 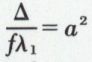 et
et  l’équation (3) devient soit
l’équation (3) devient soit  soit
soit 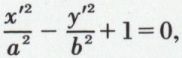 qui sont, l’une et l’autre, l’équation d’une hyperbole d’axes ωx′ et ωy′.
qui sont, l’une et l’autre, l’équation d’une hyperbole d’axes ωx′ et ωy′.
Exemple. Pour réduire l’équation 34x2 – 24xy + 41y2 + 116x – 188y + 46 = 0, on prend comme nouvelle origine le point ω (x0 = – 1, y0 = 2), x0 et y0 étant solution du système 17x – 6y + 29 = 0, 12x – 41y + 94 = 0 (fx′ = fy′ = 0), les formules de changement d’axes étant x = X – 1, y = Y + 2, ce qui donne l’équation 34X2 – 24XY + 41Y2 – 200 = 0. Les nombres λ1 et λ2 sont racines de l’équation λ2 – 75S + 1 250 = 0 : on obtient λ1 = 25 et λ2 = 50 ; d’où l’équation 25x′2 + 50y′2 = 200, ou x′2 + 2y′2 = 8, ou 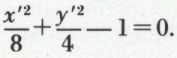 La courbe obtenue est l’ellipse réelle de centre ω (– 1 ; 2), de demi-axes
La courbe obtenue est l’ellipse réelle de centre ω (– 1 ; 2), de demi-axes 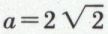 et b = 2, portés par ωx′ et ωy′.
et b = 2, portés par ωx′ et ωy′.
Réduction des coniques à direction asymptotique double
Pour l’équation 
B2 – AC = 0 ; par suite, l’équation λ2 – (A + C)S + AC – B2 = 0 qui donne les valeurs propres de la matrice  se réduit à λ2 – (A + C)S = 0 et admet une racine nulle λ = 0 et une racine non nulle λ1 = A + C. Sans changer l’origine, on choisit l’axe OX suivant la direction asymptotique double, dont un vecteur unitaire est un vecteur propre de la matrice
se réduit à λ2 – (A + C)S = 0 et admet une racine nulle λ = 0 et une racine non nulle λ1 = A + C. Sans changer l’origine, on choisit l’axe OX suivant la direction asymptotique double, dont un vecteur unitaire est un vecteur propre de la matrice 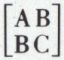 correspondant à la valeur propre λ = 0, et l’axe OY suivant la direction perpendiculaire, dont un vecteur unitaire est un vecteur propre de la matrice
correspondant à la valeur propre λ = 0, et l’axe OY suivant la direction perpendiculaire, dont un vecteur unitaire est un vecteur propre de la matrice 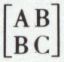 correspondant à la valeur propre λ1 ≠ 0. L’équation (1) devient alors
correspondant à la valeur propre λ1 ≠ 0. L’équation (1) devient alors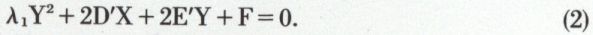
1° Si D′ ≠ 0, l’équation (2) devient λ1y′2 + 2D′x′ = 0, puis
en posant  puis
puis 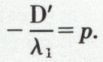 L’équation (3) est celle d’une parabole de paramètre p et de sommet
L’équation (3) est celle d’une parabole de paramètre p et de sommet 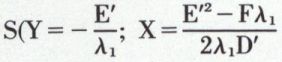 dans le système OXY).
dans le système OXY).
2° Si D′ = 0, l’équation (2) est celle de deux droites parallèles à OX.
Exemple. L’équation x2 + 2xy + y2 + 2x – y + 1 = 0, qui s’écrit (x + y)2 + 2x – y + 1 = 0, se réduit finalement à  car AC – B2 = 0, S1 = 2, les vecteurs unitaires de OX et OY étant respectivement les vecteurs
car AC – B2 = 0, S1 = 2, les vecteurs unitaires de OX et OY étant respectivement les vecteurs 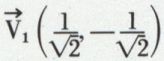 et
et 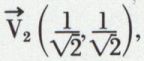 et les coordonnées du sommet étant, dans la base XOY,
et les coordonnées du sommet étant, dans la base XOY,  et
et 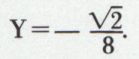 Pratiquement, on reconnaît l’équation d’une parabole au fait que AC – B2 = 0. Si l’on veut obtenir rapidement l’équation de l’axe et de la tangente au sommet de la parabole, on introduit un paramètre λ dans l’équation de la parabole, de la façon suivante :
Pratiquement, on reconnaît l’équation d’une parabole au fait que AC – B2 = 0. Si l’on veut obtenir rapidement l’équation de l’axe et de la tangente au sommet de la parabole, on introduit un paramètre λ dans l’équation de la parabole, de la façon suivante :
(x + y)2 + 2x – y + 1 ≡ (x + y + λ)2 + 2(1 – λ)x – (1 + 2λ)y + 1 – λ2 = 0 ;
puis, on dispose de λ de façon que les deux droites d’équation
x + y + λ = 0 et 2(1 – λ)x – (1 + 2λ)y + 1 – λ2 = 0
soient perpendiculaires, ce qui se produit, en supposant les axes rectangulaires, si
on obtient alors l’axe 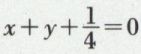 et la tangente au sommet,
et la tangente au sommet, 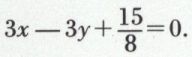 Le sommet est l’intersection de ces deux droites.
Le sommet est l’intersection de ces deux droites.
Hyperbole rapportée à certains de ses éléments
Hyperbole rapportée à ses axes
Le système d’axes xoy est supposé orthonormé.
L’hyperbole H1 a pour équation 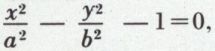 avec OA = OA′ = a, OB = OB′ = b ; A et A′ sont les sommets de l’hyperbole, Ox est l’axe transverse, ou focal, Oy est l’axe non transverse. Le faisceau des droites D1 et D2, asymptotes de l’hyperbole, a pour équation
avec OA = OA′ = a, OB = OB′ = b ; A et A′ sont les sommets de l’hyperbole, Ox est l’axe transverse, ou focal, Oy est l’axe non transverse. Le faisceau des droites D1 et D2, asymptotes de l’hyperbole, a pour équation 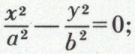 D1 et D2 ont pour équations respectives
D1 et D2 ont pour équations respectives 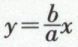 et
et 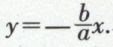 L’hyperbole H2 est l’hyperbole conjuguée de H1 : l’axe transverse de l’une est l’axe non transverse de l’autre et elles ont mêmes asymptotes. L’équation de H2 est
L’hyperbole H2 est l’hyperbole conjuguée de H1 : l’axe transverse de l’une est l’axe non transverse de l’autre et elles ont mêmes asymptotes. L’équation de H2 est  Les points F et F′ sont les foyers de l’hyperbole, FF′ = 2c est la distance focale et c2 = a2 + b2. L’hyperbole H1 est aussi l’ensemble des points M tels que | MF – MF′ | = 2a.
Les points F et F′ sont les foyers de l’hyperbole, FF′ = 2c est la distance focale et c2 = a2 + b2. L’hyperbole H1 est aussi l’ensemble des points M tels que | MF – MF′ | = 2a.
Hyperbole rapportée à ses asymptotes
En choisissant deux axes OX et OY portés par les asymptotes de l’hyperbole, les modules des vecteurs unitaires des quatre axes ox, oy, OX et OY étant égaux, l’équation de l’hyperbole est 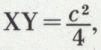 avec
avec  et
et  On tire de cette équation quelques conséquences simples.
On tire de cette équation quelques conséquences simples.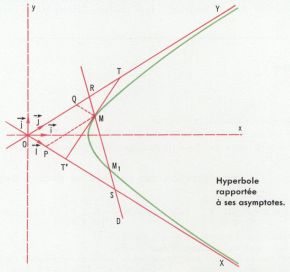
1. Quand une droite D, coupant les asymptotes en R et S, varie en gardant une direction fixe, les produits  et
et 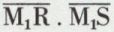 restent constants et égaux.
restent constants et égaux.
2. La droite D étant quelconque, RM = SM1, ou encore les segments RS et MM1 ont même milieu.
3. Le point de contact M d’une tangente à l’hyperbole est le milieu du segment TT′ déterminé par les asymptotes sur cette tangente. On déduit de cette propriété une méthode de construction des points d’intersection d’une droite et d’une hyperbole définie par ses asymptotes et un point.




