combinatoire (analyse)

Dénombrement des différentes dispositions que l’on peut former à l’aide des éléments d’un ensemble fini, ces éléments pouvant être discernables, partiellement discernables ou non discernables.

L’ensemble considéré, dont les éléments sont désignés par des lettres, peut être constitué :
— de n lettres deux à deux distinctes : a, b, c,..., s ;
— de p groupes différents constitués de lettres indiscernables :

avec α₁ + α₂ + ... + α_p = n ;
— de n lettres identiques.

Les dispositions classiques sont les arrangements, les permutations, les combinaisons, avec ou sans répétitions.

Groupements sans répétitions

Arrangement simple

On appelle ainsi toute disposition ordonnée de p objets choisis parmi n objets discernables, un objet figurant une fois au plus dans un même arrangement, avec

Par exemple, avec les trois lettres de l’ensemble {a, b, c}, on peut former les six arrangements des lettres prises deux à deux : (a, b), (a, c), (b, a), (b, c), (c, a), (c, b). Deux arrangements distincts de n objets pris p à p peuvent différer soit par la nature des éléments qui y figurent, soit simplement par l’ordre de ces éléments. Ainsi, les arrangements (a, b) et (a, c) sont distincts, mais les arrangements (a, b) et (b, a) sont aussi distincts.

On désigne par 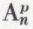le nombre des arrangements de n objets pris p à p. Le calcul de 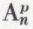, fondé sur la relation de récurrence conduit à

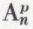est le produit de p nombres décroissants à partir de n. Ainsi : c’est le nombre de couples ordonnés que l’on peut former avec n objets distincts.

Permutation simple

On appelle ainsi toute disposition de n objets distincts.

Si deux telles dispositions sont distinctes, elles ne peuvent différer que par l’ordre des éléments qui y figurent et non par la nature de ces éléments, car on dispose de n objets et on les prend tous pour les disposer dans tous les ordres possibles. Avec les lettres de l’ensemble {a, b, c}, on peut former les six permutations suivantes : (a, b, c), (a, c, b), (b, a, c), (b, c, a), (c, a, b), (c, b, a). On désigne par P_n le nombre des permutations de n objets. En remarquant que on arrive à
P_n = n (n – 1) ... 3.2.1.
P_n est le produit des n premiers nombres entiers.

Fonction Factorielle. C’est l’application de ℕ dans ℕ (ensemble des entiers naturels), notée et définie par 0! = 1, ... (n + 1)! = (n + 1).n! Ainsi : 2! = 2.1 = 2 ; 3! = 3.2.1 = 6 ; ... ; n! = n (n – 1) ... 3.2.1. Cette notation permet d’écrire

Exemples : 4! = 24 ; 5! = 120 ; 6! = 720 ; 7! = 5 040 ; 8! = 40 320 ; 9! = 362 880 ; 10! = 3 628 800 ; 10! est, par exemple, le nombre de façons de placer dix convives autour d’une table en U.

Combinaison simple

On appelle ainsi toute partie à p éléments pris parmi les n objets distincts d’un ensemble fini, avec

Comme les n objets sont distincts, une combinaison ne peut pas contenir deux éléments identiques. De plus, l’ordre dans lequel on place les objets d’une même combinaison est indifférent. Par suite, deux combinaisons distinctes diffèrent par la nature d’au moins un de leurs éléments. C’est ainsi qu’avec les lettres de l’ensemble {a, b, c} on peut former les combinaisons (a, b), (b, c) et (c, a) des lettres deux à deux. On désigne par ou le nombre des combinaisons de n objets pris p à p. Si l’on remarque qu’à une combinaison de n objets pris p à p correspond p! arrangements des mêmes objets pris p à p (puisque le nombre des permutations de p objets est égal à p!), on voit que

Par exemple, on peut former dix parties distinctes de trois éléments avec cinq éléments distincts.

Propriétés des coefficients Elles sont nombreuses.

car on peut former une partie à zéro élément avec un ensemble contenant n éléments quel que soit n ; c’est la partie vide.

car à toute partie à p éléments correspond une partie à n – p éléments et réciproquement.

c’est la formule qui permet d’engendrer le triangle arithmétique de Pascal. Celui-ci permet le calcul, de proche en proche et pour des valeurs de n pas trop grandes, des coefficients 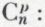chaque coefficient est égal à la somme des deux coefficients qui sont immédiatement au-dessus de lui à droite et à gauche.
Ainsi :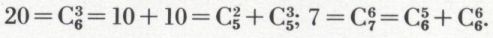

La symétrie du triangle est due à la relation

On retrouve dans ces développements les coefficients du triangle de Pascal. On peut écrire, par exemple,

De façon plus générale,

C’est la formule du binôme de Newton, et l’on appelle les coefficients les coefficients du binôme.

Groupements avec répétitions

Arrangement avec répétition

On appelle ainsi toute disposition ordonnée de p objets choisis parmi n objets distincts, chacun de ces n objets pouvant figurer jusqu’à p fois dans la même disposition. Avec les deux lettres de l’ensemble {a, b}, on peut former les quatre arrangements avec répétitions (a, a), (a, b), (b, a), (b, b) des lettres deux à deux. On peut très bien avoir p > n, car on peut répéter un même objet autant de fois que l’on veut dans une même disposition. Si l’on remarque que, pour réaliser une telle disposition, on a n possibilités pour choisir le premier objet, n possibilités pour choisir le deuxième, ..., n possibilités pour choisir le p-ième, on voit qu’il y a n^p dispositions possibles.

Exemple. Un numéro du réseau téléphonique parisien comporte sept chiffres choisis parmi les dix chiffres de l’ensemble E = {0, 1, 2, ..., 9}. Composer un numéro, c’est déterminer un arrangement avec répétitions de dix objets pris sept à sept. La capacité du réseau téléphonique parisien est donc
n^p = 10⁷ = 10 000 000 de lignes.

Permutation avec répétition

On appelle ainsi pour un ensemble formé de n objets partiellement discernables

une disposition ordonnée de tous ces objets, deux permutations avec répétitions distinctes ne pouvant différer que par l’ordre des objets.

Le nombre p_r de ces permutations a pour valeur

C’est ainsi qu’avec les chiffres 1, 1, 2, 3, 3 on peut former

Plus généralement, il y a façons de partager n objets en r groupes de telle manière que le premier groupe en contienne α₁, le deuxième α₂, ..., le r-ième α_r.