cinématique (suite)

Mouvements élémentaires

Les mouvements élémentaires du solide sont différents de ceux du point.

• Mouvement de translation. Le mouvement le plus simple d’un solide est celui dans lequel toute droite AB joignant deux points quelconques de ce solide reste constante en grandeur et en direction, c’est-à-dire constamment parallèle à elle-même. Un tel mouvement est une translation. Les vitesses de A et de B demeurent constamment identiques et, comme A et B sont arbitrairement choisis, tous les points du solide sont animés de vitesses égales et parallèles. Dans un mouvement de translation, la cinématique du solide ne diffère pas de celle d’un point quelconque de ce solide. Si le mouvement de ce point est rectiligne, la translation est dite « rectiligne » ; s’il est, en outre, uniforme, la translation est dite « rectiligne et uniforme ».

• Mouvement de rotation autour d’un axe. Si deux points A et B d’un solide sont fixes, il en est de même de tous les points de la droite AB, et le solide ne peut que tourner autour de cette droite, qui est appelée axe de rotation. Un point quelconque décrit un cercle qui a son centre sur l’axe et dont le plan est perpendiculaire à l’axe. Si ω est la vitesse angulaire de ce mouvement circulaire, la valeur de ω est la même pour tous les points du corps.

• Mouvement parallèle à un plan. Dans la rotation autour d’un axe, les vitesses de tous les points sont parallèles à un plan perpendiculaire à l’axe. Plus généralement, dans un mouvement défini par la seule condition que toutes les vitesses soient constamment parallèles à un même plan fixe (P), si l’on abaisse d’un point quelconque A du solide la perpendiculaire AB sur le plan, le point B se déplace en même temps que A. La vitesse de A est perpendiculaire à AB par hypothèse ; celle de B dans le plan (P) est également perpendiculaire à AB. Les vitesses des extrémités de AB ont donc des projections nulles sur AB, et la longueur AB est invariable. Le point A se meut dans un plan parallèle à (P), et la section déterminée dans le solide par un plan parallèle à (P) est constamment formée des mêmes points. L’étude du mouvement du solide se ramène dans ce cas à celle du mouvement d’une figure plane dans son plan. Le déplacement élémentaire d’une figure plane dans son plan peut être regardé comme produit par une rotation infiniment petite autour d’un certain centre instantané de rotation, et le déplacement continu équivaut à celui que fournit le roulement sans glissement d’une courbe mobile invariable sur une courbe fixe appelée base du roulement, la courbe mobile entraînant avec elle la figure donnée. Le centre instantané de rotation est, à chaque instant, au point de contact des deux courbes.

• Mouvement épicycloïdal. Le roulement d’une courbe mobile sur une courbe fixe s’appelle mouvement épicycloïdal, et l’épicycloïde est la courbe décrite par un point de la figure mobile. La cycloïde est un cas particulier de l’épicycloïde, quand la courbe fixe est une droite et la courbe mobile un cercle. Un autre cas particulier intéressant est celui où la base du roulement est un cercle, ainsi que la courbe mobile que l’on désigne souvent sous le nom de roulante. La roulette est la courbe décrite par un point du plan mobile ; elle est dite allongée si le point du plan mobile qui la décrit est extérieur à la roulante et raccourcie si ce point est intérieur à la roulante ; on l’appelle parfois cuspidale, lorsque le point est situé sur la roulante elle-même. Enfin, parfois, lorsque le cercle mobile est extérieur au cercle fixe ou lorsque le cercle fixe est à l’intérieur du cercle mobile, la courbe engendrée prend plus particulièrement le nom d’épicycloïde ; elle prend celui d’hypocycloïde lorsque le cercle mobile est intérieur au cercle fixe. Un cas courant de tracé d’une cycloïde est celui d’un point de la roue d’un cycliste roulant en ligne droite à une vitesse V. En cas de mauvais temps, le cycliste est maculé par la boue qui se détache de la roue arrière, bien que fuyant devant les projections de boue qu’il provoque ; s’il accélère sa vitesse pour échapper aux projections, il s’en trouve au contraire maculé davantage. En effet, dans le mouvement, le point le plus bas de la roue a une vitesse nulle et le point le plus haut une vitesse horizontale double de celle du cycliste, donc égale à 2V, et, quels que soient les efforts du cycliste, la boue, qui se détache au point le plus haut, va à sa rencontre avec une vitesse égale à 2V – V, soit V. La théorie du mouvement d’un plan sur un plan a une grande importance pratique. Elle est, en particulier, à la base de l’étude des engrenages. Pour déterminer la formule fondamentale donnant la vitesse angulaire ω de rotation autour du centre instantané de rotation, en fonction des rayons de courbure de la base et de la roulante, et de la vitesse de déplacement du centre instantané sur sa base, on considère une base AB et une courbe roulante A′B′ qui, au temps t, touche AB au point C, centre instantané de rotation ; soient R et R′ les rayons de courbure respectifs des deux courbes au point C, supposés de sens contraire. Au bout du temps dt, un point C′₁ de A′B′ vient se placer en C₁ sur la base, et les deux courbes se touchent alors en C₁. À ce moment, le point de la courbe roulante, qui était d’abord en C, se trouve amené dans une position C′. On peut imaginer que, pour amener la courbe roulante de la première position à la seconde, on la fasse d’abord tourner autour de C d’un angle égal à celui des normales C′₁N′₁ et C₁N₁ qui doivent être amenées en prolongement l’une de l’autre, et qu’on imprime ensuite à la figure une translation parallèle à CC′, de manière à amener le point C de la roulante dans la position voulue. Les arcs C′C′₁ et CC₁ étant égaux par hypothèse, la translation CC′ est infiniment petite du second ordre et ne joue donc aucun rôle au point de vue des vitesses. Celles-ci sont exactement les mêmes que si le système tournait autour du point C rigoureusement fixe, avec une vitesse angulaire ω. Soit ds la valeur commune des arcs CC₁ et C′C′₁ ; les normales C₁N₁ et C′₁N′₁ forment respectivement avec la normale initiale NN′ des angles 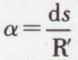et La rotation totale γ est la somme de ces angles : γ = α + β, c’est-à-dire

En divisant par dt les deux membres de cette équation, on a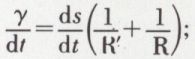

or, 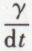est la vitesse angulaire ω et 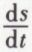la vitesse v du centre instantané de rotation sur la base ; donc

Si les rayons de courbure des deux courbes étaient de même sens, on écrirait :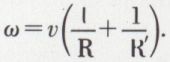

Vitesse U d’un point quelconque P de la figure mobile. Soit p la distance de P au centre C ; la vitesse du point P est U = ωp. Si l’on pose