calcul des propositions (suite)

La règle ci-après donne la façon d’éliminer ⋁. Elle repose sur les considérations suivantes. La sous-déduction m₁ à m_n fait que, si P est vraie, M est vraie, tandis que, si P est fausse, on ne peut rien conclure sur M. Il en est de même pour Q en vertu de la sous-déduction l₁ à l_j. Mais, comme, par hypothèse, P ⋁ Q est supposée vraie, il est exclu que P et Q soient toutes deux fausses. En conséquence, soit grâce à P, soit grâce à Q, soit même grâce à P et à Q, M est vraie.

Il n’est pas nécessaire de se donner des règles pour la biconditionnelle, si l’on se souvient que p ≡ q est équivalente à (p ⊃ q) ⋀ (q ⊃ p). On se contentera donc de poser
P ≡ Q = df (P ⊃ Q) ⋀ (Q ⊃ P).

Considérons maintenant une classe de propositions {P₁, P₂, ..., P_n}. S’il est possible d’en déduire, par les règles du système, une proposition P, nous écrirons
P₁, P₂, ..., P_n ⊩ P.
{P₁, P₂, ..., P_n} est la classe d’hypothèses dont P est déduite.

Exemple. p ⊃ q, q ⊃ m ⊩ pm.

La déduction s’effectue comme suit :

Certaines propositions ont ceci de remarquable qu’elles peuvent être déduites de la classe d’hypothèses vide. Nous écrirons alors ∅ ⊩ P ou, plus simplement. ⊩ P.

Par définition, toute proposition qui est déductible de la classe d’hypothèses vide est un théorème du calcul. Comme le montre la déduction ci-dessus. La proposition p ⊃ (q ⊃ p) est un théorème ; donc ⊩ p ⊃ (q ⊃ p). Une telle déduction constitue une preuve de sa dernière ligne. Elle est caractérisée par le fait que le trait vertical le plus à gauche ne porte aucune petite barre horizontale.

L’ensemble des théorèmes que l’on peut prouver à l’aide des règles hyp, rep, reit, rep df ; ⊃i, ⊃e, ⋀i, ⋀e, ⋁i et ⋁e constitue la logique absolue.

La négation

La négation permet d’élargir la logique absolue de plusieurs façons selon les règles que l’on s’accorde. Posons d’abord les trois règles qui jouent un rôle clé :

Comme on le voit, la règle correspond au raisonnement par l’absurde : si une hypothèse P conduit à une contradiction, savoir Q et cette hypothèse doit être niée.

La logique absolue, enrichie de la règle constitue la logique minimale (Johansson, 1936). Il est possible d’y effectuer la déduction suivante : Il s’agit là d’une forme affaiblie du principe classique ex falso quodlibet sequitur, affaiblie en ce sens que la proposition déduite n’est pas quelconque : il s’agit nécessairement d’une proposition négative.

La négation de la logique minimale est connue sous le nom de réfutabilité. La raison en est la suivante. Chaque fois que l’on applique la déduction logique à un domaine déterminé, il est possible de préciser au moins une proposition jugée inacceptable dans ce domaine. Désignons par F la disjonction de ces propositions. On montre, dans ces conditions, que la négation de la logique minimale peut se définir par

En d’autres termes, une proposition est niée si et seulement si elle conduit à F. Toute proposition « négative » est donc ici constructivement réfutable.

Si l’on élargit maintenant la logique minimale en introduisant la règle on obtient la logique intuitionniste (Heyting, 1930). La négation de cette logique est dite absurdité, en ce sens que les hypothèses permettent de déduire n’importe quelle proposition Q, tant affirmative que négative. La logique intuitionniste est remarquable en ceci que le principe du tiers exclu 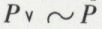ne lui appartient pas. Elle joue un rôle décisif dans le constructivisme qui caractérise la mathématique dite aussi intuitionniste.

Enfin, si l’on élargit encore la logique intuitionniste en posant la règle c’est-à-dire en s’accordant le droit d’éliminer une double négation, on obtient la logique classique, qui admet en particulier le principe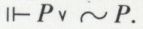

Remarques.

1. Les logiques absolue, minimale, intuitionniste et classique sont emboîtées les unes dans les autres, en ce sens que tout théorème de l’une est un théorème des suivantes, sans que la réciproque ne soit vraie.

2. On peut imaginer d’autres sous-logiques de la logique classique, en particulier la logique stricte de Curry (1952). Celle-ci peut être obtenue à partir de la logique absolue en ajoutant la règle et le principe ⊩ P ⋁

3. Glivenko (1929) a démontré que si ⊩ P est un théorème de la logique classique, est un théorème de la logique intuitionniste et réciproquement.

4. Appelons logique positive l’ensemble des théorèmes de la logique classique qui ne contiennent pas de négation. Il est très remarquable que celle-ci ne coïncide pas avec la logique absolue. Cela signifie que des propositions comme p ⋁ (p ⊃ q) ou ((p ⊃ q) ⊃ p) ⊃ p, qui appartiennent à la logique positive, mais pas à la logique absolue, exigent, pour être démontrées, le détour d’un raisonnement par l’absurde.

Quelques lois usuelles de la déduction

Sauf en quelques domaines particuliers, comme la mathématique intuitionniste et, éventuellement, la théorie des quanta, le raisonnement suit la logique classique, dans la mesure tout au moins où il se fait sans opérateurs modaux (v. logiques modales). Cela signifie que les déductions procèdent selon les règles ci-dessus et selon d’autres règles qui en dérivent. Certaines d’entre elles sont d’un usage si fréquent qu’il est utile de les rapporter.

En voici d’abord cinq que Diogène Laërce attribue à Chrysippe (281-205) :

D’autres permettent d’éliminer ou d’introduire des foncteurs dans un contexte négatif.

Lois de Morgan (1806-1871) :

D’autres enfin sont très commodes dans le raisonnement mathématique.