calcul des propositions (suite)

La forme normale disjonctive complète de p ≡ q, au sein des propositions composées des deux atomes p et q, est donc La distributivité propre au treillis booléen fait que cette expression est encore équivalente à On a alors une conjonction de disjonctions élémentaires. D’une façon générale, à toute proposition moléculaire P correspond une conjonction de disjonctions élémentaires, qui lui est équivalente et qu’on appelle sa forme normale conjonctive complète.

Les formes normales jouent un rôle important dans l’étude des propriétés du calcul des propositions. Elles montrent aussi que le calcul peut se contenter des trois foncteurs ⋁ et ⋀. La forme normale disjonctive des treize autres leur sert alors de définition. Si l’on remarque encore que

donc que

on voit que les deux foncteurs et ⋀ peuvent suffire. On pourrait aussi choisir et ⋀ en vertu de l’équivalence

La paire et ⊃ pourrait aussi suffire, puisqu’on a l’équivalence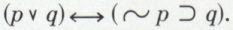

Il est même possible de définir tous les foncteurs à l’aide d’un seul d’entre eux, soit (0 1 1 1) noté donc |, soit (0 0 0 1) que nous noterons ↓. La table suivante montre comment s’y prendre :

La déduction

Les tautologies expriment des lois logiques. Toutefois, et sans faire de psychologisme, il faut remarquer que raisonner consiste non pas à appliquer des tautologies, mais à passer d’une proposition ou d’un ensemble de propositions à d’autres propositions. La question est donc de déterminer quelles sont les règles de déduction qui permettront, en particulier, d’établir les tautologies.

Notons tout d’abord qu’une proposition quelconque P, atomique ou moléculaire, peut être envisagée à titre d’hypothèse, en vue d’en déduire les conséquences possibles. Cela signifie que, jusqu’à plus ample informé, on va la tenir pour vraie. Convenons donc qu’il est toujours légitime de poser P en hypothèse et notons la chose conformément au schéma ci-dessous. Le nombre n indique à quel pas d’une déduction la règle a été utilisée, le trait vertical accompagne la déduction qui découle de l’hypothèse, la petite barre horizontale sépare l’hypothèse de ses conséquences, et le sigle hyp renvoie à la règle qui autorise de poser P.

Une déduction se déroulé pas à pas. Cela signifie que, pratiquement, chaque conséquence s’écrit après la précédente et que le processus réclame un certain temps. En droit, cependant, une déduction constitue une chaîne de propositions qui est atemporelle. Cela veut dire que, une fois écrite, une proposition P l’est pour tout le reste de la déduction. En d’autres termes, P peut être répétée à volonté au cours de la déduction, ce que stipule la règle rep.

Comme la règle hyp n’est soumise à aucune restriction d’emploi, il est possible de l’utiliser plusieurs fois au cours d’une déduction. Ce qui est acquis sous une hypothèse P le restera sous une hypothèse Q ultérieure. Il s’agit là d’un cas particulier de répétition, que nous appellerons une réitération et qui est postulé par la règle reit. Formellement, réitérer une proposition, c’est la récrire après lui avoir fait traverser au moins une barre verticale. La distinction entre répéter et réitérer sera utile au niveau de la logique des prédicats (v. calcul des prédicats).

Enfin, il est souvent commode d’introduire des définitions abréviatives. Ainsi, on écrira par exemple p ≡ q au lieu de (p ⊃ q) ⋀ (q ⊃ p). Puisque le système autorise à répéter une proposition P, il est évident qu’il doit aussi autoriser à remplacer P par toute proposition Q qui est égale à P par définition. C’est ce que stipule la règle rep df.

Ces généralités posées, voyons comment procéder à des déductions. D’un point de vue extérieur et formel, deux cas peuvent se présenter : ou bien la conséquence immédiate d’une ou de plusieurs prémisses contient un nouveau foncteur propositionnel, ou bien, au contraire, un foncteur a disparu. Dans le premier cas, on dira que l’on a appliqué une règle d’introduction et, dans le second cas, une règle d’élimination.

La logique absolue

Nous allons commencer par postuler des règles d’introduction et d’élimination pour quelques foncteurs binaires. Comme la visée est de retrouver, au titre de théorème, les tautologies, les règles devront être postulées de telle sorte qu’elles soient en accord avec les tables de vérité des foncteurs considérés.

Commençons par la conjonction dont la table est (1 0 0 0). Il est alors clair que, si P ⋀ Q est vraie, chacune des propositions P et Q est vraie. Il est donc possible de formuler les deux règles d’élimination ci-après, règles dans lesquelles le trait horizontal pointillé indique que ce qui est au-dessus de lui constitue la prémisse de la règle.

On voit aussi que, pour qu’une conjonction soit vraie, chacune des propositions qui la compose doit être vraie ; d’où la règle ⋀i. Cette règle exige donc deux prémisses, mais, comme aucune condition n’est placée sur les nombres n et m, l’ordre des prémisses n’est pas pris en considération. Cela implique que, à partir des prémisses P et Q, on peut conclure aussi bien à P ⋀ Q (n, m, ⋀i) qu’à Q ⋀ P (m, n, ⋀i).

Étudions maintenant la conditionnelle P ⊃ Q dont la table est (1 0 1 1). Faire l’hypothèse P, c’est supposer que P est vraie. Si l’on passe de P à Q par des règles, comme celles de ce système, qui conservent la vérité, la proposition Q sera vraie sous l’hypothèse P. On pourra donc affirmer « si P alors Q » comme une proposition vraie. C’est ce que pose la règle ci-après. Le premier trait vertical indique que la règle est utilisable n’importe où au cours d’une déduction. La proposition P ⊃ Q écrite en retrait de P et de Q ne dépend plus de l’hypothèse P, puisqu’elle l’inclut en elle. Enfin, la justification de la règle ⊃i se fait au nom de toute la sous-déduction n à m ; d’où la notation n — m.

L’élimination de ⊃ ne fait aucune difficulté. La table (1 0 1 1) montre en effet que si
val (P ⊃ Q) = val (P) = 1,
on a la garantie que val (Q) = 1. De là la règle ⊃e, classiquement connue sous le nom de règle du modus ponens, ou règle de détachement.

La table de la disjonction non exclusive ⋁, soit (1 1 1 0), montre que, sitôt que l’un des deux termes de P ⋁ Q est vrai, la valeur du second n’importe plus. On aura donc les deux règles ci-dessous, qui permettront d’introduire un foncteur ⋁ dans une déduction.