vectoriel sur un corps commutatif (suite)

Somme directe

Un espace vectoriel E est somme directe des sous-espaces vectoriels de la famille (Xi)_i ∈ I en nombre fini si tout élément x de l’espace E s’écrit d’une façon et d’une seule sous la forme 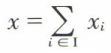avec x_i ∈ X_i, ∀i ∈ I. Pour que l’espace vectoriel E soit somme directe des sous-espaces X_i, il faut et il suffit que 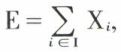c’est-à-dire que l’espace E soit engendré par les sous-espaces X_i et que pour tout i ∈ I ; ce qui signifie que l’espace X_i et l’espace engendré par les sous-espaces X_j, pour j < i, sont disjoints.

Dépendance et indépendance linéaires

Une famille (a_i)_i ∈ I finie d’éléments d’un espace vectoriel E sur un corps K est dite libre si toute relation de la forme λ_i ∈ K entraîne ∀i ∈ I, λ_i = 0. Une famille (a_i)_i ∈ I quelconque d’éléments de l’espace vectoriel E est libre, si chacune de ses sous-familles finies est libre. Une famille qui n’est pas libre est dite liée. Les éléments d’une famille libre sont dits linéairement indépendants. Les éléments d’une famille liée sont dits linéairement dépendants. Si une famille (a_i)_i ∈ I est liée, il existe des λ_i ∈ K non tous nuls, tels que par exemple, λ₀ ≠ 0 ; d’où

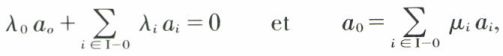
avec

Exemples.

• Dans E = ℝ[x], la famille {1, x, x², ..., xⁿ, ...}, formée des monômes de degré quelconque, est libre.

• Dans le plan rapporté à un repère quelconque trois vecteurs quelconques sont liés ; on a, par exemple,

La notion d’indépendance linéaire est très importante. Elle conduit à celle de base.

Base d’un espace vectoriel E

Elle est constituée par toute famille ℬ libre et génératrice. Cela signifie que tout élément x de l’espace E se met sous la forme (a_i)_i ∈ I désignant la base, les λ_i étant tous nuls, sauf un nombre fini d’entre eux. Les propriétés suivantes sont équivalentes :
ℬ est une base ; ℬ est une partie génératrice de l’espace E minimale pour l’inclusion : il n’existe aucune partie ℬ′ ⊂ ℬ, ℬ′ ≠ ℬ qui soit génératrice ; ℬ est une partie libre de l’espace vectoriel E maximale pour l’inclusion : il n’existe aucune partie ℬ′ ⊃ ℬ, ℬ′ ≠ ℬ qui soit libre.

Exemples de bases.

• Dans ℝⁿ, l’ensemble ℬ des éléments de la forme e_i = (δ_ij), où δ_ii = 1 et δ_ij = 0, pour j ≠ i, constitue une base, puisque 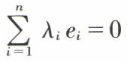entraîne λ_i = 0 et que tout élément x de l’espace E se met sous la forme

• Dans ℝ[x], ℬ = {1, x, x², ..., xⁿ, ...} est une base.

• Toute partie libre X de l’espace E est une base du sous-espace vectoriel qu’elle engendre.

Espace vectoriel de dimension finie

On appelle ainsi tout espace vectoriel possédant un système fini de générateurs. Si G est un système fini de générateurs d’un espace vectoriel E et si L est une partie libre contenue dans ce système, il existe une base B de l’espace E telle que
L ⊂ B ⊂ G.

Si L₁ est une partie libre de l’espace E, non nécessairement contenue dans le système G, G ∪ L₁ = G₁ est un système de générateurs de l’espace E. En appliquant le résultat précédent à L₁ et à G₁, on voit qu’il existe une base de l’espace E contenant la partie L₁ et contenue dans G ∪ L₁ : c’est le théorème d’échange.

Propriétés.

• Dans un espace vectoriel E de dimension finie, toutes les bases sont finies et ont le même nombre d’éléments.

• L’entier égal au nombre d’éléments d’une base quelconque de l’espace vectoriel E, s’appelle la dimension de cet espace vectoriel, notée dim_K E ou dim (E).

• La dimension de l’espace vectoriel engendré par une famille d’éléments de l’espace E s’appelle le rang de cette famille.

• Toute partie libre d’un espace vectoriel E de dimension finie n a au plus n éléments ; toute partie génératrice de l’espace E a au moins n éléments. Toute partie libre qui possède n éléments est une base ; toute partie génératrice qui possède n éléments est une base.

• Tout sous-espace vectoriel X d’un espace vectoriel E de dimension n est au plus de dimension n ; si ce sous-espace est de dimension n, il est identique à l’espace vectoriel E.

• Tout sous-espace d’un espace de dimension finie admet un sous-espace supplémentaire.

Espace dual d’un espace vectoriel E sur un corps commutatif K

C’est un espace vectoriel ℒ (E, K) des applications linéaires de l’espace E dans le corps K, noté E*. Les éléments de E* s’appellent les formes linéaires sur E.

Si f ∈ E* et x ∈ E, f(x) est un élément de K que l’on note < x, f >. L’application de E × E* dans K, qui, au couple (x, f), fait correspondre le scalaire < x, f >, vérifie les propriétés suivantes :

Ces propriétés montrent que < x, f > est une forme bilinéaire sur E × E*.

Si l’espace vectoriel E est de dimension finie, l’espace dual E* est aussi de dimension finie, et l’on a dim E* = dim E. Si dim E = n et si (e₁, e₂, ..., e_n) est une base de l’espace vectoriel E, une base de E* est de façon que 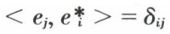(δ_ii = 1 et δ_ij = 0, pour i ≠ j), ou, sous une autre forme, et 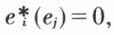pour j ≠ i. Si x ∈ E, où x_i ∈ K. Il résulte des propriétés des formes pour i = 1, 2, ..., n, que

Si f ∈ E*, telle que 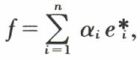on a

puisque, parmi les n² termes 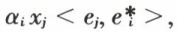il n’y en a que n qui peuvent être non nuls. Ainsi, une forme linéaire sur E est une expression linéaire à coefficients dans K. C’est ainsi que, dans E = ℝ³, f = 2x + 3y – z est une forme linéaire.

La base de E* est dite base duale de la base (e₁, e₂, ..., e_n) de E.