Se dit de tout ensemble E muni à la fois :
— d’une loi de groupe commutatif, notée additivement ;
— d’une loi de composition externe, notée 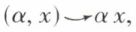 qui est une application de l’ensemble produit K × E dans E, K étant un corps commutatif, telle que :
qui est une application de l’ensemble produit K × E dans E, K étant un corps commutatif, telle que :

1 désignant l’élément unité du corps K.
Un tel ensemble est un espace vectoriel sur le corps commutatif K. Le corps K est souvent appelé le corps des scalaires de l’ensemble E. On désigne par O à la fois le zéro du groupe additif E et le zéro du groupe additif du corps de K. Cela n’entraîne aucune ambiguïté.
Des axiomes définissant un espace vectoriel, on tire les conséquences immédiates suivantes :

O désigne dans les relations (1) et (4) le zéro de l’ensemble E et dans les relations (2) et (3) le zéro du corps K.
Enfin, l’égalité λx = 0 entraîne soit λ = 0, soit x = 0 (λ ∈ k et x ∈ E) ; car, si λ ≠ 0,  existe et
existe et  ce qui entraîne x = 0, puisque 1 . x = x.
ce qui entraîne x = 0, puisque 1 . x = x.
Exemples d’espaces vectoriels.
Si x = (xi), pour i = {1, 2, ..., n}, désigne le point de l’ensemble produit ℝn, c’est-à-dire le point de coordonnées (x1, x2, ..., xn), l’ensemble ℝn, muni de l’addition définie par (x + y) = (xi + yi) et de l’opération externe αx = (αxi), α ∈ ℝ, est un espace vectoriel sur le corps des réels ℝ. Pour n = 1, 2 ou 3, on obtient respectivement la droite réelle, le plan ou l’espace à trois dimensions.
L’ensemble des polynômes à une variable à coefficients réels, muni de l’addition des polynômes et de la multiplication par un réel, constitue un espace vectoriel sur le corps ℝ. Il en est de même des fonctions continues sur [0, 1] ou des fonctions continues et dérivables sur [0, 1].
Sous-espaces vectoriels
On appelle sous-espace vectoriel d’un espace vectoriel E sur un corps K tout sous-ensemble A de cet espace, tel que :
— le sous-ensemble A soit un sous-groupe additif de l’espace E ;
— pour tout α ∈ K et pour tout x du sous-ensemble A, on ait αx ∈ A.
Le sous-ensemble A est donc une partie de E telle que les restrictions des lois de E à A confèrent à A une structure d’espace vectoriel.
Si (Ai)i ∈ I est une famille de sous-espaces vectoriels de l’espace vectoriel E et si  est l’intersection des sous-espaces de cette famille, A est aussi un sous-espace vectoriel de l’espace E, car, si x ∈ Ai et y ∈ Ai, pour tout i ∈ I, x + y ∈ A et αx ∈ Ai pour tout i ∈ I entraîne αx ∈ A.
est l’intersection des sous-espaces de cette famille, A est aussi un sous-espace vectoriel de l’espace E, car, si x ∈ Ai et y ∈ Ai, pour tout i ∈ I, x + y ∈ A et αx ∈ Ai pour tout i ∈ I entraîne αx ∈ A.
Si X est une partie de l’espace vectoriel E, il existe des sous-espaces vectoriels de cet espace contenant X, ne fût-ce que l’espace E. L’intersection de tous ces sous-espaces est un sous-espace de l’espace E, appelé sous-espace vectoriel engendré par X : c’est le plus petit sous-espace contenant X, noté Vect (X). Toute combinaison linéaire d’éléments de X, c’est-à-dire tout élément de la forme  où αi ∈ K et ai ∈ X, les éléments αi étant tous nuls, sauf un nombre fini d’entre eux, appartient à Vect (X). Inversement, l’ensemble des combinaisons linéaires d’éléments de X constitue un sous-espace vectoriel de l’espace E, contenant X ; c’est donc Vect (X). On a :
où αi ∈ K et ai ∈ X, les éléments αi étant tous nuls, sauf un nombre fini d’entre eux, appartient à Vect (X). Inversement, l’ensemble des combinaisons linéaires d’éléments de X constitue un sous-espace vectoriel de l’espace E, contenant X ; c’est donc Vect (X). On a :
Vect (X ∪ Y) = Vect (X) + Vect (Y) ;
Vect (X ∩ Y) ⊂ Vect (X) ∩ Vect (Y), avec Vect (∅) = {0} ;
si X ⊂ Y, Vect (X) ⊂ Vect (Y) ;
enfin, Vect [Vect (X)] = Vect (X).
Exemple de sous-espace vectoriel.
Dans l’espace ℝ[x] des polynômes à coefficients réels à une variable x, l’ensemble des polynômes de degré inférieur ou égal à deux est un sous-espace engendré par la partie {1, x, x2} de ℝ[x].
Sous-espaces supplémentaires
Deux sous-espaces X1 et X2 de l’espace vectoriel E sont dits supplémentaires si X1 ∩ X2 = ∅ et si tout élément x de l’espace E peut se mettre sous la forme x = x1 + x2, où x1 ∈ X1 et x2 ∈ X2. On note alors X1 + X2 = E ; x1 est la projection de x sur X1, parallèlement à X2, ou x1 est la composante de x dans X1. Les composantes x1, et x2 sont uniques. En effet, s’il existait deux décompositions  on aurait
on aurait  ce qui est impossible si
ce qui est impossible si  car alors X1 et X2 auraient en commun un élément non nul, ce qui est contraire à l’hypothèse X1 ∩ X2 = {0}.
car alors X1 et X2 auraient en commun un élément non nul, ce qui est contraire à l’hypothèse X1 ∩ X2 = {0}.
Exemples.
• Dans ℝ3 rapporté à un repère quelconque, un plan et une droite non contenue dans ce plan sont deux sous-espaces supplémentaires, par exemple le plan d’équation x + y + z = 0 et la droite d’équations x = y = z. On peut prendre le même plan et la droite d’équations x – y = 0, z = 1. Un même sous-espace peut admettre plus d’un sous-espace supplémentaire.
• L’espace vectoriel E est l’espace ℝ[x] des polynômes à coefficients réels à une variable x ; X1 est le sous-espace de ℝ[x] des polynômes de degré inférieur ou égal à deux ; X2 est le sous-espace de ℝ[x] des polynômes sans terme constant, sans terme du premier ni du second degré.
• L’espace vectoriel E est l’espace ℱ (ℝ, ℝ) des fonctions numériques réelles définies sur ℝ ; X1 est le sous-espace des fonctions paires, et X2 celui des fonctions impaires. Toute fonction f ∈ ℱ se décompose en f = P + J de façon que

Si, dans l’espace vectoriel E, les deux sous-espaces X1 et X2 sont supplémentaires, l’espace E est dit somme directe de X1 et X2. On généralise cette notion.





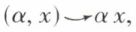 qui est une application de l’ensemble produit K × E dans E, K étant un corps commutatif, telle que :
qui est une application de l’ensemble produit K × E dans E, K étant un corps commutatif, telle que :

 existe et
existe et  ce qui entraîne x = 0, puisque 1 . x = x.
ce qui entraîne x = 0, puisque 1 . x = x. est l’intersection des sous-espaces de cette famille, A est aussi un sous-espace vectoriel de l’espace E, car, si x ∈ Ai et y ∈ Ai, pour tout i ∈ I, x + y ∈ A et αx ∈ Ai pour tout i ∈ I entraîne αx ∈ A.
est l’intersection des sous-espaces de cette famille, A est aussi un sous-espace vectoriel de l’espace E, car, si x ∈ Ai et y ∈ Ai, pour tout i ∈ I, x + y ∈ A et αx ∈ Ai pour tout i ∈ I entraîne αx ∈ A. où αi ∈ K et ai ∈ X, les éléments αi étant tous nuls, sauf un nombre fini d’entre eux, appartient à Vect (X). Inversement, l’ensemble des combinaisons linéaires d’éléments de X constitue un sous-espace vectoriel de l’espace E, contenant X ; c’est donc Vect (X). On a :
où αi ∈ K et ai ∈ X, les éléments αi étant tous nuls, sauf un nombre fini d’entre eux, appartient à Vect (X). Inversement, l’ensemble des combinaisons linéaires d’éléments de X constitue un sous-espace vectoriel de l’espace E, contenant X ; c’est donc Vect (X). On a : on aurait
on aurait  ce qui est impossible si
ce qui est impossible si  car alors X1 et X2 auraient en commun un élément non nul, ce qui est contraire à l’hypothèse X1 ∩ X2 = {0}.
car alors X1 et X2 auraient en commun un élément non nul, ce qui est contraire à l’hypothèse X1 ∩ X2 = {0}.