thermodynamique (suite)

Pour un échantillon de gaz dans lequel le nombre N des molécules, le volume V et l’énergie U sont donnés, Boltzmann pose que toutes les complexions sont également probables, que la probabilité W d’un état macroscopique est mesurée par le nombre de complexions qui lui correspondent et que l’état qui correspond à l’équilibre statistique du gaz est celui pour lequel la probabilité W est maximale.

Le nombre de complexions correspondant à un état donné est
W = N!/N₁! · N₂! ..., N_i!,
N₁, N₂ ..., N_i étant les nombres de molécules dans les domaines 1, 2 ..., i ; ces nombres étant tous très grands, la formule d’approximation de J. H. Stirling pour une factorielle conduit à :

La recherche du maximum de W conduit alors à une formule de répartition des molécules entre les divers domaines de la forme 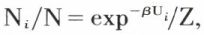où U_i est l’énergie des molécules du domaine i et 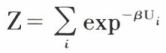une expression que l’on nomme fonction de partition, et qui joue un grand rôle en mécanique statistique.

On passe de l’étude précédente aux applications thermodynamiques, et en particulier au calcul des fonctions caractéristiques du système, à l’aide de la formule célèbre S = k · Log W, due à Boltzmann (1896) et qui pose une relation linéaire entre l’entropie S d’un état et le logarithme de la probabilité W correspondant à cet état (on remarquera simplement qu’une telle relation est cohérente avec le caractère additif de l’entropie, d’une part, et du logarithme d’une probabilité, d’autre part). Le coefficient k de proportionnalité est la constante de Boltzmann, homogène à une entropie et que l’application aux gaz parfaits montre égale au quotient R/ℜ de la constante des gaz parfaits par le nombre d’Avogadro.

L’introduction de la température thermodynamique par la relation dS = dU/T, qui caractérise une transformation du système à volume constant, permet d’identifier avec 1/kT le coefficient β de la fonction de partition, laquelle s’écrit alors et permet sous cette forme de retrouver en particulier la formule de Boltzmann qui, pour un gaz en équilibre thermique, donne l’abondance relative des molécules, dont l’énergie diffère d’une quantité donnée ΔE de l’énergie thermique moyenne, ainsi que la loi de distribution, dite de Maxwell-Boltzmann, des vitesses moléculaires u, abstraction faite de leur orientation :

(v. gaz), où M est la masse molaire du gaz ; la figure de la page précédente indique cette distribution pour l’azote à 0 °C ; l’aire colorée représente, pour un écart Δu à partir de u, la valeur de ΔN_u/N.

À côté de résultats importants obtenus par la statistique classique, certaines difficultés se sont présentées, relatives en particulier à l’expression de l’entropie et qui tiennent à la façon dont est fait le décompte des complexions correspondant à un état macroscopique donné, décompte essentiellement fondé sur l’hypothèse de la discernabilité des molécules d’un échantillon d’un corps pur, hypothèse infirmée par l’expérience ; aussi a-t-on dû apporter à la statistique classique des corrections portant sur la façon d’évaluer la probabilité d’un état macroscopique donné, et cela en tenant compte à la fois de la quantification de l’énergie et de l’indiscernabilité des molécules, notions introduites par les théories quantiques. Dans cet esprit, on renonce à numéroter les N molécules et l’on imagine que chacun des domaines de la théorie classique, correspondant à une énergie donnée des molécules, est subdivisé en cellules, dont la « dimension » est fixée par le principe d’incertitude de Heisenberg* et dont le nombre g pour un domaine, ordre de dégénérescence, représente le nombre des états distincts — c’est-à-dire discernables à l’aide d’une action extérieure — des molécules de même énergie. L’existence et le nombre des états microscopiques correspondant à un état macroscopique donné proviennent alors uniquement de la possibilité de modifier à l’intérieur de chaque domaine la répartition des N_i molécules de ce domaine entre ses g_i cellules. Ce nombre d’états dépend évidemment d’une hypothèse concernant le nombre maximal de molécules à admettre dans chaque cellule : la statistique quantique de Bose-Einstein, dont le domaine d’application concerne les particules de spin nul ou entier (bosons), n’émet à ce sujet aucune hypothèse restrictive, alors que la statistique de Fermi-Dirac, applicable aux particules de spin demi-entier (fermions), fait l’hypothèse — dérivée du principe d’exclusion de Pauli* — suivant laquelle toute cellule est ou bien vide ou bien complètement occupée par une particule seulement. Il en résulte dans ces deux statistiques des expressions différentes de la probabilité d’un état macroscopique, de l’état le plus probable et de la fonction de partition.

On peut, de là, comme précédemment dans la statistique classique, passer aux applications thermodynamiques à l’aide de la relation S = k · Log W et obtenir pour un gaz parfait, sous certaines réserves d’approximations, des expressions des fonctions thermodynamiques communes aux deux statistiques. L’expression de l’entropie, dite formule de Sackur-Tetrode, ne contient pas de constante arbitraire, présente le caractère d’additivité propre à une extensité et conduit, aux basses températures, à de bonnes vérifications expérimentales, qualités que ne possède pas celle que la statistique classique permet d’obtenir.

L’intérêt des statistiques, principalement des statistiques quantiques, est considérable. On ne peut, ici, qu’énumérer succinctement quelques-uns des domaines de la physique dans lesquels les théories statistiques ont joué un grand rôle dans l’explication et la prévision des phénomènes :
— le phénomène de condensation d’Einstein pour un gaz parfait, auquel s’applique la statistique de Bose et dont la transition⁴HeI → ⁴HeII semble bien être un exemple ;
— l’étude à très basse température des propriétés de³He, lequel, contrairement à⁴He, est un fermion ;
— l’étude du comportement des électrons (qui sont aussi des fermions) dans les métaux ;
— l’application première de la statistique de Bose aux photons et à la théorie du rayonnement thermique du corps noir ;
— pour les solides, les théories de la chaleur spécifique, développées par Einstein, puis par Peter Joseph William Debye (1884-1966), la théorie du paramagnétisme à basse température, etc.