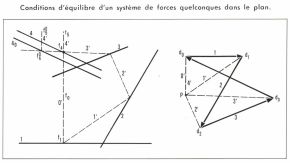
Conditions d’équilibre d’un système de forces dans le plan

La condition de fermeture du polygone dynamique, nécessaire dans tous les cas d’équilibre, n’est plus suffisante lorsque les forces ne sont pas concourantes. Une seconde condition graphique (équivalente à l’annulation du moment résultant par rapport à un point quelconque du plan) doit encore être satisfaite. Étant donné le polygone dynamique de quatre forces (de lignes d’action 1, 2, 3 et 4) qui se ferme, c’est-à-dire que son origine d₀ et son extrémité d₄ coïncident, les rayons polaires 0′ et 4′ coïncident ; par suite, dans le funiculaire correspondant, les côtés extrêmes f₀f₁ et 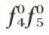sont parallèles. Le système de forces considéré est donc équivalent à deux forces dirigées suivant ces côtés et respectivement équipollentes 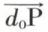à et à c’est-à-dire à un couple. Telle est la conséquence mécanique de la fermeture du dynamique envisagée seule. Pour qu’il y ait équilibre, il faut, en outre, que les deux forces auxquelles a été réduit le système se détruisent, ce qui exige que le premier et le dernier côtés du funiculaire coïncident (donc que le côté 3′ de ce funiculaire vienne passer par le point de rencontre du côté 0′ de la ligne d’action 4). Il faut donc que le funiculaire se ferme, comme le dynamique. Pour qu’un système de forces coplanaires soit en équilibre, il faut et il suffit que le dynamique de ces forces et le funiculaire pour un pôle quelconque du plan se ferment tous deux. Comme le choix de P est arbitraire, si le funiculaire se ferme pour un point P, il se fermera nécessairement pour un pôle P′. La condition de fermeture du funiculaire équivaut à l’annulation des moments résultants du système des forces par rapport à un point P quelconque du plan.

Décomposition d’une force suivant trois lignes d’action non concourantes

Soit la force , définie par sa ligne d’action 4 et le vecteur équipollent 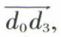à décomposer en trois forces, , 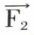et 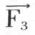, suivant les lignes d’action 1, 2 et 3 ; ces forces seront entièrement connues quand on aura déterminé leurs vecteurs équipollents 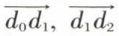et Ce problème peut être résolu soit au moyen du polygone dynamique seul, soit par l’emploi combiné du polygone dynamique et du polygone funiculaire.

• Solution par l’emploi du polygone dynamique seul. On joint le point de rencontre R des droites 4 et 1 au point de rencontre S des droites 2 et 3 par une droite dont on désignera la direction par l. On peut d’abord décomposer la force 4 suivant les directions 1 et l par le tracé du polygone dynamique d₀d₁d₃, dont les côtés ont les directions 1 et l pour la composante dirigée suivant l, dont la grandeur est donnée par d₁d₃, suivant les directions 2 et 3 par le tracé du dynamique d₁d₂d₃, dont les côtés ont les directions 2 et 3. Les trois composantes cherchées sont données, en grandeur et en direction, par les vecteurs 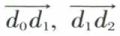et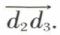

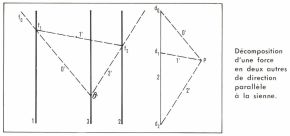
Décomposition d’une force en deux autres de direction parallèle à la sienne

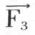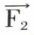Soit la force , dont la ligne d’action est 3 et le vecteur équipollent à décomposer suivant les lignes 1 et 2, parallèles à 3. Si l’on fait choix d’un pôle P quelconque, les directions 0′ et 2′ des rayons polaires aboutissant en d₀ et en d₂ sont celles des côtés extrêmes du polygone funiculaire servant à composer les forces et en 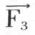. Si l’on se donne le point θ de ces côtés extrêmes sur la ligne d’action 3 (où ils doivent se couper) et si l’on mène par ce point θ des parallèles aux directions 0′ et 2′, on obtient sur 0 et 2 les points f₁ et f₂, qu’il suffit de joindre pour avoir la direction 1′. La parallèle à cette direction 1′ menée par P donne sur le dynamique (ici réduit à la droite d₀d₂) le point d₁. Les vecteurs et font connaître les composantes demandées en grandeur et en sens. Si, au lieu de décomposer 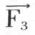suivant 1 et 2, il s’agissait de l’équilibrer au moyen de deux forces dirigées suivant ces lignes d’action, il suffirait de renverser le sens de ces vecteurs, c’est-à-dire de prendre d₁d₀ et d₂d₁.

M. D.

➙ Mécanique / Statique / Vecteur.

 G. Pigeaud, Résistance des matériaux et élasticité (Gauthier-Villars, 1920) ; Cours de mécanique appliquée (Gauthier-Villars, 1923). / H. Bouasse, Statique (Delagrave, 1921). / M. D’Ocagne, Cours de géométrie pure et appliquée de l’École polytechnique (Gauthier-Villars, 1924). / R. Brard, Cours de mathématiques appliquées (École polytechnique, 1943). / Soc. acad. Hütte, Des Ingenieurs Taschenbuch (Berlin, 1951-1955, 5 vol. ; trad. fr. Manuel de l’ingénieur, Béranger, 1960-1962, 2 vol.).