série numérique (suite)
• Pour que la série un, soit convergente, il faut et il suffit que la suite Sn = u0 + u1 + ∙∙∙ + un, soit majorée. En effet, la suite Sn majorée et croissante, puisque Sn + 1 – Sn = un + 1 > 0, admet une limite S qui est la borne supérieure des quantités Sn.
• Si, à partir d’un certain rang n0, les deux séries un et vn sont telles que 
alors :
— si la série vn converge et a pour somme S′, la série un converge et a pour somme 
— si la série un diverge, il en est de même de la série vn.
Ce critère de comparaison prend la forme suivante plus souple et plus facilement utilisable. Si les deux séries un et vn sont telles que, pour n assez grand, le rapport 
soit défini et admette une limite finie k quand n → + ∞, la convergence de la série vn entraîne celle de la série un. Si k ≠ 0, les deux séries un et vn sont de même nature. En effet, si 
quand n → ∞, il existe n0 ∈ ℕ tel que n > n0 entraîne 
ou
Cela montre, d’après la première forme du critère, que la série un converge si la série Wn = (k + ε) vn converge, et diverge si la série 
diverge, ces deux séries étant de même nature que vn. La série un est donc de même nature que la série vn. Par exemple, les deux séries 
sont de même nature, car, quand n → ∞, le rapport 
Cette comparaison peut servir à trouver la nature de l’une des deux séries, connaissant celle de l’autre. Chacune des deux peut en effet être étudiée séparément : la série un est une série de Riemann convergente et la série vn peut être étudiée directement.
• Une condition suffisante de convergence, pour la série un, est qu’il existe une série convergente vn et un nombre k > 0 tel que 
En effet, de l’inégalité 
on déduit
puisque la série vn converge vers une limite S′. Comme la suite Sn est croissante et majorée par kS′, elle converge.
• Si, pour 
les deux séries un et vn sont telles que 
et si la série vn est convergente, il en est de même de la série un. Par suite, si la série un est divergente, il en est de même de la série vn, sinon, la série un convergerait. En effet, si pour 
on en déduit, par récurrence, que 
pour tout 
Ainsi, pour 
et on peut appliquer la condition suffisante donnée ci-dessus.
• On peut appliquer ce dernier critère d’une façon plus souple et sous une forme pratique. C’est le critère de d’Alembert.
Si la série de terme général un est telle que le rapport 
soit défini et admette une limite finie l,
— si l < 1, la série un est convergente ;
— si l > 1, la série un est divergente, car son terme général ne tend pas vers zéro.
En effet, si l < 1, il existe n0 tel que la condition n > n0 entraîne 
On peut alors appliquer le critère précédent avec vn = (l + ε)n. La série un converge, car la série vn est une série géométrique de raison r = l + ε < 1, donc convergente.
Si 
on ne peut rien conclure, sauf si la limite 1 est atteinte par valeurs supérieures, cas où la série diverge.
• Critère de Cauchy. Ce critère est l’un de ceux qui viennent le plus naturellement à l’esprit. La première série que l’on étudie est la série géométrique, un = λn, qui ne converge que si λ < 1 et dont la somme est 
On est alors tenté de chercher si on peut trouver un nombre λ vérifiant, pour tout n ∈ ℕ, l’inégalité 
ce qui permettra de conclure à la convergence de la série un si λ < 1. Pour trouver ce nombre λ, s’il existe, on étudie la quantité 
Or, celle-ci dépend de l’entier n et ne conduit pas à un nombre λ indépendant de n. Mais la limite de 
si elle existe, peut être indépendante de n. On obtient ainsi le critère de convergence sous la forme suivante :
— si, quand n → + ∞, 
la série un est convergente ;
— si 
la série un diverge, car son terme général ne tend pas vers zéro.
En effet, si 
il existe n0 tel que, pour n > n0,
Il en résulte que 
pour n > n0, avec λ = l + ε, ce qui entraîne la convergence de la série.
• Utilisation des séries de Riemann. Ces séries ont pour terme général la quantité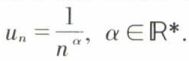 
Elles sont convergentes pour α > 1 et divergentes pour 
Par suite, pour que la série de terme général un soit convergente, il suffit qu’il existe un nombre réel α > 1 tel que nα un, soit majoré ; pour qu’elle soit divergente, il suffit qu’il existe un nombre réel k > 0 tel que, pour n > n0, 
les séries vn et wn étant de même nature et convergentes. Il en résulte que la série un converge. En revanche, si 
les séries vn et wn étant divergentes. Le critère utilisant les séries de Riemann est connu sous le nom de règle nα un.
Séries entières
Une série entière de la variable complexe z est une série dont le terme général est de la forme un = anzn, n ∈ ℕ, (an) désignant une suite donnée de nombres complexes. L’étude de la série un = anzn consiste à déterminer le sous-ensemble D du plan de la variable complexe z à l’intérieur duquel la série est absolument convergente. Il existe un nombre réel R positif, éventuellement nul ou infini tel que :
— si R = 0, la série anzn ne converge que pour z = 0 ;
— si R = + ∞, la série anzn converge absolument pour tout z ∈ ℂ ;
— si R est un nombre fini non nul, la série anzn est absolument convergente pour |z| < R et divergente pour |z| > R.
Le nombre R est appelé rayon de convergence. Si R ≠ 0, le disque ouvert D (O, R) de centre O et de rayon R est le disque ou cercle de convergence ; l’intervalle ouvert ] – R, + R[ de la droite réelle ℝ est l’intervalle de convergence. La détermination de R se fait par l’étude d’une série à termes positifs et, comme un = anzn, les règles de Cauchy et de d’Alembert se prêtent aisément à cette détermination. Si 
lim sup désignant la plus grande des limites de 
quand n → + ∞,
Par suite,
— si L = + ∞, la série anzn diverge quel que soit z ≠ 0 ;
— si L = 0, la série anzn converge quel que soit z ∈ ℂ ;
— si 0 < L < + ∞, la série anzn converge pour tout z tel que 
Ainsi,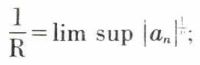
c’est la formule d’Hadamard.
Si la suite 
tend vers une limite L, quand n → + ∞, le rayon de convergence de la série anzn est 