résistance des matériaux (suite)
Règles applicables aux pièces prismatiques longues
La courbe G0G1, dont il a été précédemment question, est l’axe longitudinal de la pièce prismatique, ou fibre moyenne ; une fibre de la pièce est le volume engendré par un élément superficiel élémentaire dS de la section normale. L’aire plane S qui engendre la pièce est la section transversale, ou profil ; on appelle prisme élémentaire le volume compris entre une section normale telle que G et une section normale G′ très voisine ; la portion de fibre comprise entre ces deux sections porte le nom de fibre élémentaire. Souvent, l’axe longitudinal est une droite : on a affaire à une poutre droite, mais presque toujours l’axe longitudinal est une ligne plane ; on a alors une poutre courbe, et le plan qui contient l’axe longitudinal s’appelle plan moyen. Si la section transversale n’est pas constante, mais varie progressivement, on a alors une poutre à section variable. Lorsque les variations de section sont suffisamment faibles et très progressives, les procédés de calcul restent applicables. On suppose alors que chaque élément dS est lui-même variable, et le volume engendré par cet élément porte encore le nom de fibre. Parfois, au lieu de poutres homogènes, c’est-à-dire composées d’un seul matériau ayant le même coefficient d’élasticité, les diverses fibres sont formées de matériaux différents ; c’est le cas des éléments en béton armé ; on est alors conduit à substituer aux éléments réels dS′ de la section des éléments fictifs dS = m dS′ obtenus en multipliant les aires réelles réels dS′ par des coefficients convenables, théoriquement proportionnels aux coefficients d’élasticité des différents matériaux.

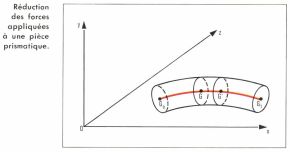
Réduction de forces appliquées à une pièce prismatique
Sur l’axe G0G1 d’une pièce prismatique, on prend un point G qui est le centre de gravité d’une section normale, dénommée également G. La section G divise la pièce en deux tronçons, l’un à gauche, entre G0 et G, et l’autre à droite, entre G et G1. L’ensemble des forces appliquées à un tronçon fait équilibre à l’ensemble des tensions exercées à travers la section G par l’autre tronçon, et inversement. Il convient d’étudier l’ensemble des forces appliquées à gauche pour avoir une notion des tensions qui s’exercent à travers la section normale G. Par translation, on transporte en G les axes de coordonnées. Comme il s’agit d’une section de faible superficie, on peut, sans inconvénient, remplacer les forces du tronçon de gauche par leur résultante R de composantes X, Y, Z et par un couple (ou moment résultant) de composantes Mx, My, Mz suivant les axes. La résultante R peut se remplacer par sa projection N sur la tangente GG′ et par sa projection T sur le plan de la section normale G. La composante N est l’effort normal et la composante T est l’effort tranchant.
De même, le couple peut être remplacé par ses deux projections sur la tangente GG′ sur le plan de section G. La projection sur GG′ porte le nom de couple de torsion, ou moment de torsion ; la composante située dans le plan de section normale est le moment fléchissant, que l’on désigne par M. L’effort normal N appliqué en G a pour effet une traction ou une compression simple ; l’effort tranchant T exerce un glissement simple, mais en général le cisaillement ou glissement ne se présente pas seul. Le couple de torsion, d’axe dirigé suivant l’axe de la pièce, exerce une torsion simple ; enfin, le moment fléchissant, couple dont l’axe est dans le plan normal (plan de la section), entraîne une flexion simple.
Effort tranchant
Si le point G′ se trouve à une distance ds de G, on a :
En prenant comme trièdre de référence un système d’axes tel que Ox coïncide avec GG′ et qu’en outre Z = 0, le plan xOy contenant l’effort tranchant T = Y au point G, on a (dy et dz étant nuls) :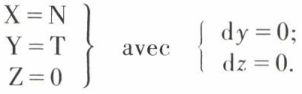
D’où :
L’effort tranchant Y est, en valeur absolue, égal au quotient, par dx, élément d’arc GG′, de l’accroissement  du moment fléchissant. Il est la dérivée du moment fléchissant prise par rapport à l’axe longitudinal.
du moment fléchissant. Il est la dérivée du moment fléchissant prise par rapport à l’axe longitudinal.
Cas particulier des poutres dont le plan moyen est vertical et qui ne sont soumises qu’à des forces appliquées situées dans ce plan moyen. Ce cas est le plus usuel. On a alors Z = 0, et aussi
Mx = My = 0.
Il n’y a plus de couple de torsion, et l’axe du couple est toujours dirigé dans le plan de la section normale. D’autre part, un système de forces situées dans un même plan se réduit en général à une force unique. En composant toutes les forces appliquées au tronçon de poutre situé à gauche de la section G, on obtient donc une force unique R définie par ses composantes X et Y et par son moment Mz, que l’on désigne habituellement par M, en posant

Théorie générale de la flexion
Pour lever l’indétermination concernant la répartition des efforts dans l’étendue d’une section transversale d’une pièce fléchie, on a recours à l’hypothèse de Bernouilli, qui est à la base de la théorie de la flexion des prismes. Pendant une déformation par flexion, une section transversale quelconque de la pièce prismatique demeure plane, identique à elle-même et normale à l’axe longitudinal de la pièce. L’expérience montre en outre que les variations de longueur dès différentes fibres de la section transversale sont proportionnelles à leur distance à une certaine droite de la section qu’on appelle axe neutre. D’après la loi de Hooke, l’intensité des tensions moléculaires normales à la section est, en chaque point, proportionnelle à la distance de ce point à l’axe neutre. C’est Navier qui a déduit ce résultat de l’hypothèse de Bernouilli. Pour déterminer l’axe neutre d’une pièce soumise à une flexion simple, il faut tracer l’ellipse centrale d’inertie de la section et déterminer le diamètre conjugué de la direction normale à l’axe du moment fléchissant.




