relation binaire (suite)
La relation inverse ou réciproque de la relation ℛ de l’ensemble E vers l’ensemble F est la relation, notée ℛ–1 telle que y ℛ–1 x ⇔ x ℛ y. Par exemple, si, dans E = F = ℕ, ℛ désigne la relation « divise », la relation inverse est « est multiple de ». En effet, x divise y si et seulement si y est multiple de x. Il est clair que (ℛ–1)–1 = ℛ.
Deux relations sont égales si elles sont vérifiées par les mêmes couples, c’est-à-dire si elles ont même graphe.
La relation ℛ est incluse dans la relation ℛ′, ou ℛ implique ℛ′ (ℛ ⇒ ℛ′) si le graphe de ℛ est inclus dans celui de ℛ′ : tout couple (x, y) vérifiant la relation ℛ vérifie aussi la relation ℛ′. On dit aussi que la relation ℛ est plus fine que la relation ℛ′.
Si ℛ1 et ℛ2 sont deux relations de l’ensemble E vers l’ensemble F, l’intersection 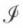 de ℛ1 et de ℛ2 est la relation telle que
de ℛ1 et de ℛ2 est la relation telle que 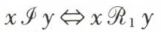 et x ℛ2 y. Le graphe de l’intersection
et x ℛ2 y. Le graphe de l’intersection est l’intersection des graphes de ℛ1 et de ℛ2.
est l’intersection des graphes de ℛ1 et de ℛ2.
De même, on définit la réunion 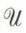 de ℛ1 etℛ2, telle que
de ℛ1 etℛ2, telle que 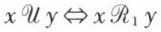 ou x ℛ2 y. Il suffit que x et y soient en relation par l’une des deux relations ℛ1 ou ℛ2 pour que x soit en relation avec y par la relation
ou x ℛ2 y. Il suffit que x et y soient en relation par l’une des deux relations ℛ1 ou ℛ2 pour que x soit en relation avec y par la relation 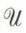 .
.
Toutes ces opérations sur les relations ne sont que des transcriptions des opérations dans un ensemble.
Si, dans trois ensembles E, F et H, ℛ est une relation de l’ensemble E vers l’ensemble F et 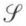 une relation de F vers H, la relation-produit, ou relation composée, de ℛ par
une relation de F vers H, la relation-produit, ou relation composée, de ℛ par 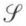 , notée
, notée 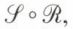 est définie comme la relation de E vers H telle que x ∈ E, z ∈ H,
est définie comme la relation de E vers H telle que x ∈ E, z ∈ H, 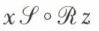 si et seulement s’il existe y ∈ F tel que x ℛ y et
si et seulement s’il existe y ∈ F tel que x ℛ y et 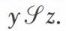 Si K est un quatrième ensemble et
Si K est un quatrième ensemble et  une relation de H vers K, le produit des relations ℛ,
une relation de H vers K, le produit des relations ℛ, 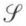 et
et  est associatif, c’est-à-dire que l’on a
est associatif, c’est-à-dire que l’on a
Propriétés éventuelles d’une relation binaire dans un ensemble E
Une relation binaire ℛ dans un ensemble E est :
— réflexive si x ℛ x pour tout élément x de l’ensemble E ;
— symétrique si x ℛ y entraîne y ℛ x ;
— antiréflexive si 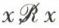 pour tout élément x de l’ensemble E,
pour tout élément x de l’ensemble E, 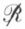 indiquant la négation de la relation ℛ ;
indiquant la négation de la relation ℛ ;
— antisymétrique ou propre si x ℛ y et y ℛ x entraînent x = y (sous une autre forme, si x ≠ y et x ℛ y, 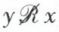 ) ;
) ;
— transitive si x ℛ y et y ℛ z entraînent x ℛ z ;
— totale si 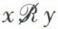 entraîne y ℛ x [quel que soit le couple (x, y), on a au moins l’une des deux relations x ℛ y ou y ℛ x] ;
entraîne y ℛ x [quel que soit le couple (x, y), on a au moins l’une des deux relations x ℛ y ou y ℛ x] ;
— circulaire si x ℛ y et y ℛ z entraînent z ℛ x.
exemples
1. Dans l’ensemble ℕ, la relation « divise » est réflexive, antisymétrique et transitive.
En effet, quel que soit l’élément x appartenant à l’ensemble ℕ, x divise x. D’autre part, si x|y, y = xx′, x′ ∈ ℕ et si y|x, yy′ = x, y′ ∈ ℕ, il en résulte que y = yy′x. D’où, puisque tous les nombres utilisés appartiennent à l’ensemble ℕ, y′x′ = 1 et, pour la même raison, y′ = x′ = 1 et y = x.
Enfin, si x|y et y|z, y = xx′ et z = yy′ ; d’où z = xx′y′ = xx″, ce qui en traîne x|z.
2. Dans l’ensemble R, la relation « strictement inférieur à » est antisymétrique et transitive.
En effet, si x < y, on n’a pas y < x. De plus, x < y et y < z entraînent x < z.
3. Dans l’ensemble ℝ, la relation « inférieur ou égal à » est réflexive, antisymétrique, transitive et totale.
En effet, pour tout élément x de l’ensemble ℝ, on a 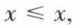 puisque x = x. Si
puisque x = x. Si 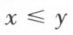 et
et 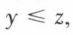 on a
on a 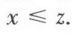 Si
Si 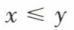 et
et 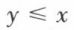 on a x = y. Enfin, étant donnés deux nombres réels quelconques x et y, on peut toujours les comparer en utilisant la relation
on a x = y. Enfin, étant donnés deux nombres réels quelconques x et y, on peut toujours les comparer en utilisant la relation 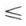 , car ou bien x = y ou bien x ≠ y, et alors x < y ou y < x.
, car ou bien x = y ou bien x ≠ y, et alors x < y ou y < x.
Relations d’équivalence dans un ensemble E
Une relation d’équivalence est une relation binaire dans un ensemble E, réflexive, symétrique, transitive.
exemple
Dans l’ensemble ℤ des entiers relatifs, la relation ℛ définie par
x ℛ y ⇔ Ǝ k ∈ ℤ : x – y = kp
(p étant un entier naturel donné) est une relation d’équivalence.
En effet, x ℛ x, car x – x = o = op. De plus, x ℛ y ⇔ x – y = kp ⇔ y – x = (– k)p = k′p, k′ = – k ; d’ou y ℛ x. Enfin, si x ℛ y et y ℛ z, c’est-à-dire si x – y = kp et y – z = k′p, en ajoutant ces deux égalités membre à membre, on obtient x – z = (k + k′) = k″p ; donc x ℛ z.
Cette relation est appelée congruence arithmétique modulo p. Elle est susceptible d’applications en arithmétique.
Classes d’équivalence
Dans un ensemble E muni d’une relation d’équivalence ℛ, la classe d’équivalence de l’élément a de l’ensemble E est formée des éléments x de l’ensemble E qui sont en relation avec a : A = {x ∈ E, x ℛ a}. Il est équivalent d’écrire x ℛ a ou a ℛ x, puisque la relation ℛ est symétrique. Comme, de plus, la relation ℛ est transitive, la classe A est aussi celle de n’importe lequel de ses éléments, et tous les éléments de la classe A sont en relation deux à deux. Si b est un élément de l’ensemble E n’appartenant pas à A, la classe B de l’élément b est distincte de celle de l’élément a, et l’on a : A ∩ B = Ø. Il est impossible que deux classes distinctes aient un élément commun, sinon elles seraient confondues. La relation ℛ détermine donc une partition de l’ensemble E, c’est-à-dire un partage de l’ensemble E en classes d’équivalence, non vides, deux à deux disjointes et dont la réunion est égale à l’ensemble E.
La notion de classe d’équivalence est très importante en raison de la partition réalisée par les classes. L’ensemble, noté E/ℛ, appelé ensemble quotient de E par ℛ est constitué par les classes d’équivalence, qui sont des parties de l’ensemble E, mais qui deviennent les éléments de E/ℛ. Grâce à des relations d’équivalence, on peut obtenir de nouveaux ensembles. Cette méthode est féconde, notamment en théorie des groupes et aboutit à des résultats très appréciés.




