projection (système de) (suite)

Le modèle terrestre n’est pas une surface développable, c’est-à-dire qu’il ne peut être appliqué sur un plan sans déchirure ni duplicature. Toute représentation plane entraîne donc des déformations ou altérations : l’altération angulaire est la différence entre l’angle de deux courbes du modèle et l’angle de leurs images planes ; l’altération linéaire est définie par l’expression m – 1 dans laquelle « m » est le module linéaire, c’est-à-dire le rapport des longueurs de deux éléments infiniment petits correspondants (dS sur le plan, ds sur le modèle). Le module linéaire est, en général, fonction non seulement du point, donc des coordonnées φ et λ, mais aussi de la direction de l’élément considéré en ce point, et il est préférable de distinguer cette notion de la notion d’échelle. L’échelle d’une carte, ou rapport entre une longueur sur la carte et la longueur réelle, n’a pas rigoureusement la même valeur en deux points quelconques ; l’échelle nominale, indiquée sur une carte, n’est rigoureuse que le long de certaines lignes, dites « automécoïques ». Mais deux cartes établies dans le même type de représentation et qui ne diffèrent que par l’échelle nominale sont deux figures semblables, et les altérations y sont identiques. Pour l’étude de ces déformations, il suffit donc d’adopter une échelle nominale 1/1 ou encore de préciser les lignes automécoïques le long desquelles le module linéaire est égal à 1.

Le problème de l’étude des déformations est entièrement résolu par la considération de l’indicatrice de Tissot (fig. 1) : celle-ci est une ellipse, image plane d’un cercle infiniment petit tracé sur le modèle et dont on considère le rayon comme unité. Le module linéaire en A dans la direction AB est alors la longueur du demi-diamètre AB de l’ellipse ; les demi-axes de l’indicatrice sont les modules principaux « m₁ » et « m₂ » ; les directions des axes sont les directions principales, images de deux directions rectangulaires du modèle.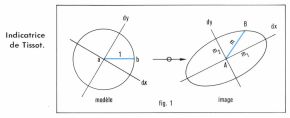

L’altération angulaire est une fonction de l’angle considéré et des quantités m₁ et m₂. L’altération des surfaces est définie par le module aréolaire, c’est-à-dire le rapport des aires de deux domaines fermés correspondants : il est égal au produit m₁ ∙ m₂.

Classification des représentations planes

• D’après les caractères locaux

• Les représentations conformes sont celles où l’altération angulaire est nulle, en tout point. Dans ces conditions, on a l’égalité
m₁ = m₂.

L’indicatrice de Tissot (fig. 1) est alors un cercle et le module linéaire est indépendant de la direction, ce qui justifie l’expression d’échelle locale. Ces propriétés montrent que deux figures infiniment petites correspondantes sur le modèle et sur le plan sont semblables, mais la similitude n’existe plus pour des figures finies.

• Les représentations équivalentes sont celles où le module aréolaire est égal à l’unité. On a alors
m₁ ∙ m₂ = 1.

L’aire de l’indicatrice de Tissot est égale à celle du cercle générateur ; l’égalité des aires se conserve pour des domaines finis.

Une représentation plane de la Terre ne peut être à la fois conforme et équivalente : les deux conditions ne sont réalisées simultanément que si la surface modèle est une surface développable.

• Les représentations qui ne sont ni conformes ni équivalentes sont dites aphylactiques.

• Une représentation est dite sécante si elle possède deux parallèles automécoïques, tangente si elle possède un parallèle automécoïque, équidistante si tous les méridiens sont automécoïques.

• D’après les caractères globaux

• Un type de représentation peut être précisé par une épithète se rapportant au canevas, c’est-à-dire à l’ensemble des images planes des méridiens et des parallèles. Dans ces conditions, une représentation est dite :
— cylindrique si les images des méridiens sont des droites parallèles et celles des parallèles des droites perpendiculaires à celles-ci ;
— méricylindrique si les images des parallèles sont des droites parallèles ;
— conique si les images des méridiens sont des droites concourantes et celles des parallèles des arcs de cercle centrés au point de concours des images des méridiens ;
— mériconique si les images des parallèles sont des arcs de cercle concentriques ;
— azimutale si les images des méridiens sont des droites concourantes et celles des parallèles des circonférences entières centrées au point de concours des images des méridiens ;
— polyconique si les images des parallèles sont des arcs de cercle non concentriques, centrés sur une droite image d’un méridien.

• Une autre épithète permet de préciser l’orientation sur un modèle sphérique de la Terre, les grands cercles issus d’un même point Q appelé pivot peuvent jouer le même rôle que les méridiens, grands cercles issus du pôle géographique P. Une représentation (fig. 2) est dite :
— directe ou polaire si le pivot est un des pôles terrestres ;
— transverse ou méridienne si le pivot est sur l’équateur ;
— oblique si le pivot est un point quelconque.

Domaines d’utilisation

Le but essentiel des représentations planes est l’établissement des cartes. Pour les cartes modernes à grandes et moyennes échelles (nominales), on utilise à peu près exclusivement les représentations conformes, qui présentent l’avantage de pouvoir être localement assimilées à une similitude, pour des figures qui ne sont pas trop grandes. Pour que l’altération linéaire ne dépasse pas une valeur fixée à l’avance on est conduit à réduire le champ de la représentation, c’est-à-dire l’étendue de la portion de surface terrestre qu’on se propose de représenter : en France, on utilise trois représentations coniques conformes (zones Lambert I, II, III). On peut aussi adopter le long de certaines lignes un module linéaire légèrement inférieur à l’unité : l’altération linéaire est négative dans certaines zones, mais reste petite en valeur absolue.